Rincón de Práctica Stata#
Elección Binaria usando Stata#
import pandas as pd
import ipystata
Ejemplo 1 Comparación LPM/Logit/Probit. (nivel usuario)#
Simular datos \(\{y^*_i,x_i\}_{i=1}^N\) para el modelo
\[y^*_i=3+9*x_i+u_i\hspace{0.6cm}i=1,...,N\]donde \(N=100\), \(u\sim\mathbb{N}(0,1)\), \(x\sim U[0,1]\) y la variable \(y^*\) es una variable latente para la cual solo se observa su contraparte \(Y=\mathbb{1}(y^*>P50(y*)))\).
Estimar los modelos LPM, Logit y Probit usando comandos de Stata.
Presentar los efectos marginales del Logit calculados manualmente (es decir, emplenado \(f_i*\beta\)). Luego presentar los efectos marginales del Logit y Probit empleando comandos simplificados de Stata.
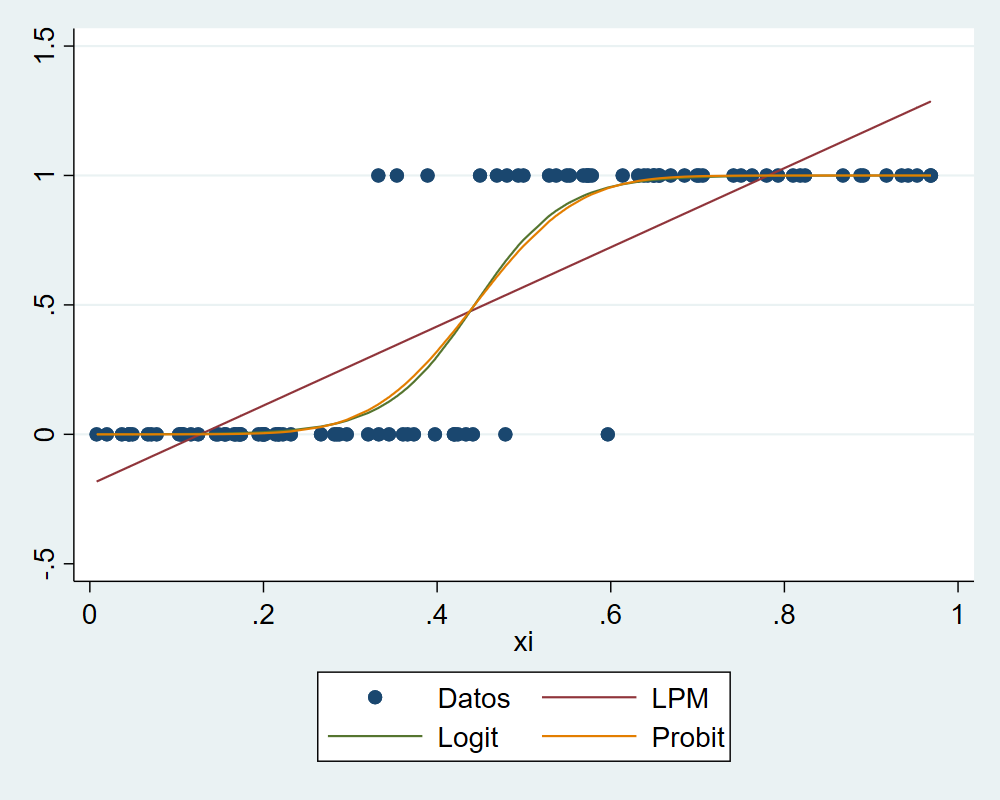
Comparar las probabilidades predichas por los modelos LPM, Logit y Probit.
%%stata
* 1. Simular datos
set seed 123
set obs 100
gen u = rnormal()
gen xi = uniform()
gen ys = 3 + 9*xi + u /* ystar: variable latente */
qui sum ys
scalar P50 = `r(mean)'
gen Y = ys>= P50
tab Y
Number of observations (_N) was 0, now 100.
Y | Freq. Percent Cum.
------------+-----------------------------------
0 | 53 53.00 53.00
1 | 47 47.00 100.00
------------+-----------------------------------
Total | 100 100.00
%%stata
* 2.Comparar LPM, Logit y Probit
eststo Model_LPM: qui reg Y xi
eststo Model_Probit: qui probit Y xi
eststo Model_Logit: qui logit Y xi
di "Tabla con coeficientes"
esttab Model_* , mtitles("LPM" "" "Logit")
* 3.Efectos marginales
* manualmente (aplicando la teoría):
qui mean xi
scalar xbar = _b[xi]
qui logit Y xi
scalar Xb = _b[_cons] + _b[xi]*xbar
di "Resultado efecto marginal computo manual f_i*beta"
display (exp(-Xb) / (1 + exp(-Xb))^2)*_b[x] /* Efecto Mg = f_i*Beta */
di "Resultado efecto marginal usando comando mfx o margins"
qui logit Y xi
mfx
qui probit Y xi
mfx
* 4. Comparación de probabilidades
qui reg Y xi
predict prob_ols
qui logit Y xi
predict prob_logit, pr
qui probit Y xi
predict prob_probit, pr
sum prob*
sort xi
twoway (scatter Y xi)(line prob_ols xi)(line prob_logit xi) (line prob_probit xi), legend(order(1 "Datos" 2 "LPM" 3 "Logit" 4 "Probit"))
Tabla con coeficientes
------------------------------------------------------------
(1) (2) (3)
LPM Logit
------------------------------------------------------------
main
xi 1.528*** 10.78*** 19.64***
(14.84) (4.76) (4.26)
_cons -0.194*** -4.778*** -8.701***
(-3.68) (-4.63) (-4.18)
------------------------------------------------------------
N 100 100 100
------------------------------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001
Resultado efecto marginal computo manual f_i*beta
4.8764782
Resultado efecto marginal usando comando mfx o margins
Marginal effects after logit
y = Pr(Y) (predict)
= .45903234
------------------------------------------------------------------------------
variable | dy/dx Std. err. z P>|z| [ 95% C.I. ] X
---------+--------------------------------------------------------------------
xi | 4.876478 1.14772 4.25 0.000 2.62698 7.12597 .434694
------------------------------------------------------------------------------
Marginal effects after probit
y = Pr(Y) (predict)
= .46345582
------------------------------------------------------------------------------
variable | dy/dx Std. err. z P>|z| [ 95% C.I. ] X
---------+--------------------------------------------------------------------
xi | 4.283179 .89792 4.77 0.000 2.52329 6.04307 .434694
------------------------------------------------------------------------------
(option xb assumed; fitted values)
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
prob_ols | 100 .47 .4172699 -.1824463 1.286371
prob_logit | 100 .47 .4456849 .000194 .9999672
prob_probit | 100 .4698878 .4442902 1.34e-06 1
Ejemplo 2 Probit. (nivel intermedio)#
Simular datos \(\{y_i,x_i\}_{i=1}^N\), con \(N=100\), en donde la variable \(y\) es binaria y \(x\sim\mathbb{N}(0,1)\).
Escribir un programa en Stata para la función de verosimilitud.
Estimar usando el comando
ml.
%%stata
* 1. Simular datos
gen x = rnormal()
gen p = normprob(x)
gen y = rbinomial(1,p)
tab y
y | Freq. Percent Cum.
------------+-----------------------------------
0 | 51 51.00 51.00
1 | 49 49.00 100.00
------------+-----------------------------------
Total | 100 100.00
%%stata
* 2. Escribir programa para la función log-likelihood
cap prog drop my_probit
pro def my_probit
args lnf mu
qui replace `lnf' = ln(normal( `mu')) if $ML_y1 == 1
qui replace `lnf' = ln(normal(-`mu')) if $ML_y1 == 0
end
* 3. Optimizar la log-likelihood
ml model lf my_probit (y = x)
ml max
di "Mismo resultado que: probit y x"
probit y x
1. args lnf mu
2. qui replace `lnf' = ln(normal( `mu')) if $ML_y1 == 1
3. qui replace `lnf' = ln(normal(-`mu')) if $ML_y1 == 0
4. end
initial: log likelihood = -69.314718
alternative: log likelihood = -76.435943
rescale: log likelihood = -69.295933
Iteration 0: log likelihood = -69.295933
Iteration 1: log likelihood = -47.969319
Iteration 2: log likelihood = -47.901947
Iteration 3: log likelihood = -47.901854
Iteration 4: log likelihood = -47.901854
Number of obs = 100
Wald chi2(1) = 28.56
Log likelihood = -47.901854 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
x | 1.115593 .2087545 5.34 0.000 .7064422 1.524745
_cons | .0563109 .1480588 0.38 0.704 -.233879 .3465008
------------------------------------------------------------------------------
Mismo resultado que: probit y x
Iteration 0: log likelihood = -69.294717
Iteration 1: log likelihood = -47.969261
Iteration 2: log likelihood = -47.901947
Iteration 3: log likelihood = -47.901854
Iteration 4: log likelihood = -47.901854
Probit regression Number of obs = 100
LR chi2(1) = 42.79
Prob > chi2 = 0.0000
Log likelihood = -47.901854 Pseudo R2 = 0.3087
------------------------------------------------------------------------------
y | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
x | 1.115593 .2087545 5.34 0.000 .7064422 1.524745
_cons | .0563109 .1480588 0.38 0.704 -.233879 .3465008
------------------------------------------------------------------------------
