Teoría Máxima Verosimilitud

MLE: Maximum Likelihood Estimation

Estimador

Estimador de Máxima Verosimilitud (MLE): Dado un conjunto de datos, \(\{w_i\}_{i=1}^n\), se busca el vector de parámetros \(\boldsymbol{\theta}\) que generen la mayor probabilidad de haber observado ese conjunto particular de datos. Es decir, el \(\boldsymbol{\theta}\) que haga más verosímil (“con apariencia de verdadero”) el resultado que hemos obtenido.

Figura: Ilustración de dos f.d.p. Fuente: Contrucción en R con datos simulados.

En particular, la especificación del estimador consta de:

• Una muestra (aleatoria): \(\{w_i\}_{i=1}^n\)

• Una función de probabilidad (f.d.p.) \(f(w_1,…,w_n; \boldsymbol{\theta})=f(\boldsymbol{w};\boldsymbol{\theta})\) (asociada a la muestra)

Diremos entonces que el modelo esta correctamente especificado si el vector de parámetros que se emplea es el verdadero (\(\theta_0\)): \(f(w_1,…,w_n; \theta_0)\). A su vez, llamaremos a \(\theta\) como un vector candidato o vector hipotético al vector de parámetros, y por ende, \(f(w_1,…,w_n; \theta)\) será una densidad hipotética.

La anterior función de distribución conjunta es empleada en ML para obtener los estimadores. La idea es encontrar el vector candidato que genere la mayor probabilidad. Se denomina a dicha función de probabilidad conjunta como función de verosimilitud ( likelihood function ) y la denotaremos por

\[\mathcal{L}_n(\theta)=f(w;\theta)\]

Es de notar que, dados los datos, esta es una función que dependerá del vector de parámetros (y está afectada por \(n\)). Es decir, la verosimilitud es básicamente la probabilidad conjunta de los datos, evaluada en la muestra observada y vista como una función de los parámetros. Así, la función objetivo a emplear para el computo de los parámetros será la de verosimilitud.

La intuición detrás de MLE de ‘querer buscar parámetros que den la mayor probabilidad’ se traduce en términos matemáticos en querer maximizar la función de verosimilitud, por lo que MLE es estimador extremo. Ahora, es de anotar que dicha función de verosimilitud puede eventualmente ser fuertemente no lineal (es la distribución de probabilidad conjunta de \(n\) observaciones independientes), lo que puede implicar desafíos en términos numéricos (computacionales). Por ende, para ayudar en este aspecto, se emplea una transformación monótona que facilite el proceso. En particular, se toma ventaja de que la función logarítmica realiza transformaciones monótonas (e.g., para \(z_1>z_2\), se tiene que \(ln(z_1)>ln(z_2)\) con \((z_1,z_2)\in\mathbb{R}^{+}\)). Así, considerando que el vector de parámetros que maximiza el logaritmo de la función de verosimilitud es el mismo que maximiza la la función de verosimilitud, se emplea como función objetivo a optimizar el logaritmo de la función de verosimilitud:

\[\mathcal{l}_n(\boldsymbol{\theta})=ln(\mathcal{L}_n(\boldsymbol{\theta}))\]

Así, el vector de parámetros MLE estará dado por

\[\hat{\boldsymbol{\theta}}_{MLE}=\text{arg max}_{\boldsymbol{\theta}}\,ln(f(\boldsymbol{w};\boldsymbol{\theta}))\]

Para despejar o resolver la expresión anterior, y encontrar el vector de parámetros estimados, se obtiene primero la función Score . Esta función es básicamente el gradiente de la log-likelihood (es decir, las condiciones necesarias de primer orden - F.O.C. ):

\[S(\boldsymbol{\theta})=\frac{\partial ln(\mathcal{L}_n(\boldsymbol{\theta}))}{\partial \boldsymbol{\theta}}\]

Errores estándar (distribución asintótica)

Definimos la matriz de información \(I(\boldsymbol{\theta})\) (o, específicamente, Matriz de Información de Fisher - Fisher Information ) como el producto interno del vector score

\[I(\boldsymbol{\theta})=\mathbb{E}\left\{S(\boldsymbol{\theta})\,S(\boldsymbol{\theta})'\right\}\]

Altos valores en \(I\) se asocian con que pequeños cambios en \(\theta\) conllevan a grandes cambios en la log-likelihood, lo que significa que hay información considerable sobre \(\theta\).

Una igualdad relevante asociada a la anterior definición es la Igualdad de la Matriz de Información, en la cual

\[\mathbb{E}_f\left\{S(\boldsymbol{\theta})\,S(\boldsymbol{\theta})'|_{\boldsymbol{\theta}_0}\right\}=-\mathbb{E}_f\left\{H|_{\boldsymbol{\theta}_0}\right\}\]

en donde \(H\) es la matriz hessiana que organiza todas las derivadas parciales de segundo orden,

\[\boldsymbol{H}=\frac{\partial^2\mathcal{L}_n(\boldsymbol{\theta})}{\partial \boldsymbol{\theta} \partial \boldsymbol{\theta}'}\]

Bajo algunas condiciones de regularidad (que definiremos adelante), se puede obtener un estimador de la matriz de varianza y covarianza mediante la matriz hessiana evaluada en los parámetros MLE:

\[\text{Var}_H(\hat{\boldsymbol{\theta}})=-\boldsymbol{H}(\hat{\boldsymbol{\theta}})^{-1}\]

alternativamente, empleando la matriz de información,

\[\text{Var}(\hat{\boldsymbol{\theta}})=I(\hat{\boldsymbol{\theta}})^{-1}\]

Distribución asintótica. Bajo los siguientes supuestos (o condiciones)

• El proceso generador de los datos es la densidad condicional \(f(\cdot)\) empleada para definir la función de verosimilitud.

• la función de densidad satisface \(f(w_i,\boldsymbol{\theta}^{(1)})=f(w_i,\boldsymbol{\theta}^{(2)})\) si y solo si \(\boldsymbol{\theta}^{(1)}=\boldsymbol{\theta}^{(2)}\) .

• La matriz

  \[\text{plim }n^{-1} H(\boldsymbol{\theta})\]

  existe y es no singular.

• Las operaciones de diferenciación e integración de la función (log) verosimilitud son reversibles.

entonces,

• \(\hat{\boldsymbol{\theta}}\) es un estimadores consistente de \(\boldsymbol{\theta}\).

• converge a tasa \(\sqrt{n}\) a una distribución normal

\[\hat{\boldsymbol{\theta}}\sim\mathbb{N}\left(\boldsymbol{\theta},-\boldsymbol{H}(\boldsymbol{\theta})^{-1} \right)\]

A partir de lo anterior, dos propiedades a resaltar del MLE son:

• Efficiencia. \(\hat{\boldsymbol{\theta}}_{MLE}\) alcanza la cota inferior de Cramer-Rao,

  \[Var(\hat{\boldsymbol{\theta}}_{MLE}(\boldsymbol{w}))\geq [I(\boldsymbol{\theta}_0)]^{-1}\]

• Invarianza. Si \(\gamma=g(\boldsymbol{\theta})\), se tiene que \(\hat{\gamma}=g(\hat{\boldsymbol{\theta}})\), para \(g(\cdot)\) continua y diferenciable.

Inferencia.

Consideramos ahora un test o prueba para inferencia estadística en el contexto de ML. Si bien bajo la premisa que la función de verosimilitud es conocida se pueden emplear varios test, algunos de ellos asintóticamente equivalentes, nos enfocaremos en el test de razón de versimilitud ( Likelihood Ratio TEST ) ya que en muchos casos es fácil de calcular.

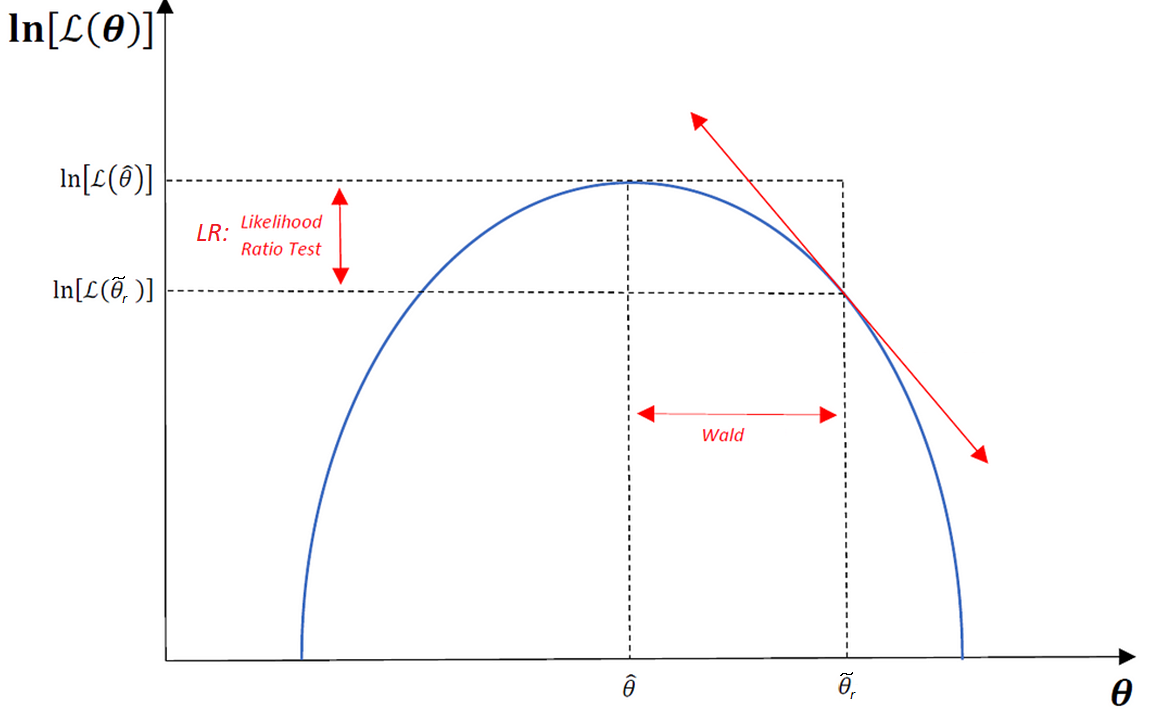
Sea \(\hat{\theta}_{u}\) el vector de parámetros que se obtendría al maximizar (el log de) la función de verosimilitud sin la restricción impuesta en la hipótesis nula, \(\text{ln }L(\theta)\). Sea \(\widetilde{\theta}_{r}\) el vector de parámetros que se obtendría al maximizar (el log de) la función de verosimilitud sujeta a la restricción (por ejemplo, \(\widetilde{\theta}_{r}-\lambda'(r-R\beta)\)). El estadístico Razón de Verosimilitudes (LR) estará definido por

\[LR=-2[\ell(\widetilde{\theta}_{r})-\ell(\hat{\theta}_{u})]\sim\chi^2_q\]

La idea del test es que si la hipótesis nula es verdadera, \(\ell(\widetilde{\theta}_{r})\) y \(\ell(\hat{\theta}_{u})\) deberían ser iguales. En otras palabras, se evalúa si la diferencia entre ambas log-likelihood functions es significativa desde un punto de vista estadístico.

Figura: Ilustración del test LR.

---

Ejemplos.

Ejemplo 1 (sobre la notación vista). Supongamos \(z_i\sim i.i.d.\,\mathbb{N}(\mu,1)\) para \(i=1,...,n\). De forma equivalente, diremos que la distribución de probabilidad es \(\phi(w_i)\), para \(w_i=(z_i-\mu)\) y \(\phi(w_i)=(2\pi)^{-1/2}exp(-w_i^2/2)\) ; es decir, la distribución normal estándar (distribución gaussiana). Por ende, en este caso, la notación que empleamos correspondería a:

• \(\theta=\mu\)

• \(f(\boldsymbol{w};\boldsymbol{\theta})=f(w_1,...,w_n;\mu)=\Pi_{i=1}^n{\phi(w_i)}\)

en donde \(\phi(\cdot)\) es la distribución nomal estandar.

Así, el estimador máximo verosímil (ML) estará dado por

\[\hat{\mu}_{MLE}=\text{arg max}_{\mu}\,\left(\sum_{i=1}^n{log\,\phi(z_i-\mu)}\right)=\text{arg max}_{\mu}\,\left(-\frac{n\cdot log(2\pi)}{2}-\sum_{i=1}^n{\frac{(z_i-\mu)^2}{2}}\right)\]

al resolver,

\[\hat{\mu}_{MLE}=\bar{z}=\frac{\sum_i z_i}{n}\]

---

Ejemplo 2. NLRM ( Normal Linear Regression Model ) Supongamos un modelo de regresión lineal como el visto en OLS : \(Y=X\beta+u\) . El conjunto de datos es \(w_i=(Y_i,X_i)\) para \(i=1,...,n\) y el vector de parámetros es \(\boldsymbol{\theta}=(\boldsymbol{\beta},\sigma^2)=(\beta_1,...,\beta_k,\sigma^2)\). Bajo el supuesto que \((Y-X\boldsymbol{\beta})=u\sim\,\mathbb{N}(0,\sigma^2I_n)\), los estimadores ML están definidos por

\[(\hat{\boldsymbol{\beta}},\hat{\sigma}^2)_{MLE}=\text{arg max}_{(\boldsymbol{\beta}\in\mathbb{R}^k,\sigma^2>0)}\,\left(-\frac{n\cdot log(2\pi\sigma^2)}{2}-\frac{(Y-X\boldsymbol{\beta})'(Y-X\boldsymbol{\beta})}{2\sigma^2}\right)\]

es decir, la log-likelihood es

\[\ell(\boldsymbol{\theta})=-\frac{n\cdot log(2\pi\sigma^2)}{2}-\frac{(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})'(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta})}{2\sigma^2}\]

al resolver (es decir, a partir de las condiciones de primer orden F.O.C. evaluadas en el estimador ML),

\[\hat{\boldsymbol{\beta}}_{MLE}=(X'X)^{-1}(X'Y) \hspace{0.5cm};\hspace{0.5cm}\hat{\sigma}^2_{MLE}=(Y-X\hat{\boldsymbol{\beta}})'(Y-X\hat{\boldsymbol{\beta}})n^{-1}\]

Notar que la expresión para \(\beta\) corresponde a la misma que se obtiene por OLS.

Además, después de resolver, se obtiene la siguiente matriz de información

\[\begin{split}I(\boldsymbol{\beta}_0)= \left[\begin{array}{cc} \frac{1}{\sigma_0^2}(X'X) & 0\\ 0 & \frac{N}{2\sigma_0^4} \end{array}\right]\end{split}\]

Esta expresión es empleada para los errores estándar.